Sistema de Numeración decimal
Símbolos del Sistema de Numeración Decimal
En la mayoría de las actividades que desarrolla el hombre necesariamente debe llegar a establecer un resultado o expresión numérica.
En la ingeniería, en la arquitectura, en la medicina, en la química, etc, las magnitudes deban expresarse en forma concreta.
Los símbolos numéricos que hoy se utilizan fueron introducidos por los matemáticas árabes, quienes los habrían tomado de los hindúes.
Los símbolos que se usan actualmente en el sistema de numeración son los siguientes:
{1,2,3,4,5,6,7,8,9,0}
A estos símbolos básicos indoarábicos se les llama también dígitos.
Características principales del Sistema de Numeración Decimal
En un numeral, cada dígito tiene un valor relativo y un valor posicional.
La base del sistema decimal es diez. Diez unidades de un orden cualquiera forman una unidad del orden
inmediatamente superior.
En un numeral, cada posición es diez veces mayor que la que está inmediatamente a su derecha
Valor posicional
El valor de los dígitos según su posición en un numeral, hasta la centena de millón, aparece en el cuadro siguiente:
Posición |
8 ª Posición |
7ª Posición |
6ª Posición |
5ª Posición |
4ª Posición |
3ª Posición |
2ª Posición |
1ª Posición |
centenas de millón |
decenas de millón |
unidades de millón |
centenas de mil |
decenas de mil |
unidades de mil |
centenas |
decenas |
unidades |
CMi |
DMi |
UMi |
CM |
DM |
UM |
C |
D |
U |
Diez unidades forman una decena.
Diez decenas forman una centena.
Diez centenas forman una unidad de mil.
Diez unidades de mil forman una decena de mil.
Diez decenas de mil forman una centena de mil.
Diez centenas de mil forman una unidad de millón.
Diez unidades de millón forman una decena de millón.
Diez decenas de millón forman una centena de millón.
En el numeral 222 el mismo dígito tiene distintos valores de acuerdo con cada posición que ocupa en el numeral 222.
2 |
2 |
2 |
2 centenas |
2 decenas |
2 unidades |
Como 1 decena = 10 unidades
1 centena = 100 unidades
Entonces, los valores del dígito 2, según su posición en el numeral son los siguientes:
2 |
2 |
2 |
2 x 100 unidades
= 200 unidades |
2 x 10 unidades
= 20 unidades |
2 unidades |
Forma exponencial de escribir un Numeral
Los valores posicionales de los dígitos
en un numeral se pueden expresar en potencias de 10.
Potencias de 10
1 =
= 100 La potencia
100 es 1
10 = 10
= 101
100
= 10 x 10
=
102
1.000 = 10 x 10 x 10
=
103
10.000 = 10 x10 x 10 x 10
= 104
100.000 = 10 x10 x 10 x 10 x 10
= 105
1.000.000 = 10 x10 x10 x 10 x 10 x 10 =
106
10.000.000 = 10 x10 x10 x10 x 10 x 10 x 10 = 107
Para cada dígito en el numeral 853.416.027 se puede establecer lo siguiente: 853.416.027
7 x 100 unidades
2 x 101 unidades
0 x 102 unidades
6 x 103 unidades
1 x 104 unidades
4 x 105 unidades
3 x 106 unidades
5 x 107 unidades
8 x 108 unidades
Así, el desarrollo exponencial del numeral 853.416.027 es:
(8 x 108) + (5 x 107) + (3 x 106) + (4 x 105) + (1 x 104) + (6 x 103) + (0 x 102) + (2 x 101) + (7 x 100)
A la inversa, a partir del desarrollo exponencial se puede establecer el respectivo numeral.
En efecto, el numeral correspondiente al desarrollo exponencial:
(3x105)+(2x1041 +(6x103)+(1 x 102)+(5x101)+(4x100) es = 326.154
puesto que:
3 x 105 = 3 x 100.000 = 300.000
2 x 104 = 2 x 10.000 = 20.000
6 x 103 = 6 x 1.000 =
6.000
1 x 102 = 1 x 100 =
100
5 x 101 = 5 x 10 =
50
4 x 100 = 4 x 1
= 4
326.154
Numeración Romana
La numeración romana es e! sistema de representación de los numerales
empleados por los romanos
Símbolos de la Numeración
Romana
la numeración romana se representa a través de los siguientes
símbolos:
I =1 C=100
V =5 D=500
X =10 M=1.000
L=50
En la numeración
romana no existe símbolo para el dígito cero.
Reglas para la representación de los numerales romanos
Un mismo símbolo no se puede repetir más
de tres veces.
Los símbolos V y L no se repiten.
Los símbolos que se repiten se suman entre sí.
Los símbolos que van a la derecha de otro mayor se suman.
Un símbolo que va a la izquierda de uno mayor que él se resta
Sólo los símbolos I, X y C se restan a otros mayores.
Equivalencia de decenas son numerales romanos vales romanos
10 = X 40 = XL
70 = LXX
20 = XX 50 = L 80
= LXXX
30 = XXX 60 = LX 90
= XC
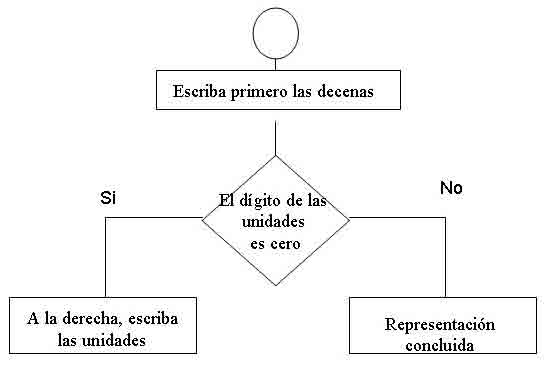
Diagrama para representar un numeral romano formado por decenas

Ejemplos:
XXX = 10 + 10 + 10 = 30
LV = 50 + 5 = 55
IC = 100 - 1 = 99
CM = 1.000 - 100 = 900
Aplicación del diagrama
Representar el numeral 12 en numerales romanos
12 = 1 decena + 2 unidades
Entonces:
1° Escribir las decenas
X
2°¿El dígito de las unidades es cero? No
A la derecha escribir las unidades
XII
Representar el numeral 30 en numeles romanos
30 = 3 decenas + 0 unidad
Entonces:
1° Escribir las decenas
XXX
2° ¿El dígito de las unidades es cero?
sí
Representación concluida
30 = XXX
Algunos Subconjuntos de IN
Números pares son los múltiplos de 2 o que son divisibles por 2.
P={x E IN /x=2n,n E IN}
Ejemplo:
P = {0, 2, 4, 6, 8, 10, ..., 2n, ...}
Números impares son aquellos que están formados por la adición de un número par y el uno.
I={x E IN/x=2n +1,n E IN}
Ejemplo:
I = {1, 3, 5, 7, 9, ..., (2n + 1), ...}
Antecesor y Sucesor de
un Número Natural
Excluyendo el cero, el antecesor de un número natural es aquel que está
inmediatamente a su izquierda en la recta numérica.
Por ejemplo:
El número que está inmediatamente a la izquierda del 1, en la recta numérica, es el 0, luego, el antecesor de 1 es 0.
___________________________________
| |
| | | |
| |
0 1 2 3 4 5 6 7
antecesor de 1
De igual forma se tiene que:
el antecesor de 3 es
2
el antecesor de 6 es 5
el antecesor de 10 es 9
El sucesor de un número natural es aquel que está inmediatamente
Por Eejemplo:
El número que está inmediatamente a la derecha del 0, en la recta
nu mérica, es el 1. Luego, el sucesor de 0 es 1.
___________________________________
| |
| | | |
| |
0 1 2 3 4 5 6 7
sucesor de 0
De igual forma se tiene que:
- el sucesor de 2 es
3
- el sucesor de 5 es 6
- el sucesor de 12 es 13
Al unir dos conjuntos
disjuntos se obtiene un tercer conjunto cuyo cardinal se denomina suma.
Los siguientes son conjuntos disjuntos:
A = {1,3,5} B = {2,4} # A=3 # B = 2 |
Al unir los conjuntos disjuntos se obtiene:
# A + B = # {A U B} 3 + 2 = 5 suma |
Los términos de la adición
se llaman sumandos y el resultado se llama suma o total:
25 } sumando
25 + 31 =
56
+ 31
sumando
Total
--------
56
Para resolver una suma de números naturales se debe ordenar los sumandos de tal modo que siempre sumen cifras del mismo orden:
unidades con unidades, decenas con decenas, centenas con centenas, etc.
Asociatividad
a, b,c E IN
(a + b) + c = a + ( b + c)
Si se agrupan los sumandos de distintas maneras, la suma no cambia.
(38 + 15) + 20 = 38 + (15 + 20)
53 + 20 = 38 + 35
73
= 73
Conmutatividad
a,b E IN
a + b = b + a
Si se cambia el orden de los sumandos; .lá suma no,varia.
18 + 3 = 3 + 18
21 = 21
Elemento neutro
a E IN
a + 0 = a
El elemento neutro es cero. `
25 + 0 = 25
Regularidad
a, b,c E IN .. ,
[a + c = b + c]=>[a = b]
Si: a dos números naturales iguales
se le sumán números naturales iguales las sumas son iguales.
[a + 5 = b + 5]=> [a = b]
Multiplicación de Números Naturales
La multiplicación de dos números naturales,excluyendo el cero, es igual a la cardinalidad del producto
cartesiano delos conjuntos que ellos representan.
Diagrama general de la multiplicación en IN
Con factores más de un dígito


División de Números
Naturales Términos de la división
Comparada con la multiplicación, la división es la operación
inversa.
Dividir un número a (dividendo) por otro número b (divisor), consiste
en dividendo
encontrar un número c (cuociente) tal que multiplicado por el divisor
dé el divisor
dividendo.
[a : b = c]<=> ra [a = b • c]
La división está resuelta en IN
sólo si el cuociente es un número natural y I residuo
el resto es cero.

Diagrama de la división en IN

Potenciación
La siguiente multiplicación tiene sus factores iguales:
5•5•5
Una multiplicación de factores iguales se llama potencia. En una potencia
se distinguen la base y el exponente.
La base es el factor que se repite y el exponente es el número que indica las veces que se repite la base como factor.
En la multiplicación 3 • 3 • 3 • 3, la base es 3 y el exponente es 4:
Exponenete
34
base
Si se tiene la potencia 23 , su desarrollo es: 2 • 2 • 2 y el valor nurriérico es 8.
Todas las potencias que tienen como base 10 se llaman potencias de 10. Algunas potencias de 10 son:
101 =10 104
= 10.000
102 = 100 105
= 100.000
103 = 1.000 106 = 1.000.000
- Potencia de cero es aquella cuyo exponente es igual a cero: 20 50
El resultado de una potencia cero de base distinta de cero es igual a 1.
20 = 1 50 = 1
- Potencia de exponente unidad es aquella potencia cuyo exponente es 1
31 71
Una potencia de exponente unidad es igual a la base
31 =
3 71 = 7
Factorización
8 • 3
= 24
factor fator Producto
los términos de una multiplicación son: factores y producto.
El producto de una multiplicación puede obtenerse con diferentes pares
de factores
8 x 3 = 24
6 x 4 = 24
1 • 24 = 24
Para cada número es posible determinar el conjunto de factores.
Por ejemplo:
Factores de 2 = {1, 2}
Factores de 3 = {1, 3}
Factores de 4 = {1, 2, 4}
Factores de 8 = {1, 2, 4, 8}
- Número primo
Es aquel que tiene solamente dos factores desiguales, el 1 y el propio número.
Ejemplos:
5 = {1, 5} 7 = {1, 7}
Reglas de la divisibilidad
Para saber si la división entre números naturales es exacta, no necesariamente habrá que resolverla.
Se pueden aplicar determinadas reglas prácticas de divisibilidad para este propósito.
- Divisibilidad por 2
Son divisibles por 2 todos los números cuyo último dígito es cero o par.
Por ejemplo:
10, 12, 14, 16, 18, 20, 22
- Divisibilidad por 3
Son divisibles por 3 todos los números cuya suma de sus dígitos es un múltiplo de 3
Por ejemplo:
360 = 3 + 6 + 0 = 9
Como 9 es múltiplo de 3, el número 360 es divisible por 3.
Por el contrario:
148 = 1 + 4 + 8 = 13
Como 13 no es múltiplo de 3, 148 no es divisible por 3.
- Divisibilidad por 6
Todos los números que son ;divisibles por 2 y 3,,también son divisibles por 6.
Por ejemplo: 144
Es divisible por 2 porque el último dígito es par (4).
Es divisible por 3 porque la suma de sus dígitos es un múltiplo de 3:
1 + 4 + 4 = 9 9 es múltipo de 3
144 es divisible por 6, puesto que es divisible por 2 y 3 a la vez.
- Divisibilidad por 4
Son divisibles por 4 todos'los números terminados en dos,;ceros o cuyos dos últimos dígitos, forman un número múltiplo de 4.
Por ejemplo:
1.500 es divisible por 4 porque termina en dos ceros.
128 es divisible por 4 porque sus dos últimos dígitos (28) forman un número múltiplo de 4.
- Divisibilidad por 5
Son divisibles por 5 todos los números cuyo último dígito es cero o cinco.
Por ejemplo:
120 es divisible por 5 porque el último dígito es cero.
135 es divisible por 5 porque el último
dígito es 5.
Divisibilidad por 9
Son divisibles por 9 todos los números cuya.suma de sus dígitos es un múltiplo de 9
Por ejemplo:
567 es divisible por 9 ya que 5
+ 6 + 7 = 18 y 18 es múltiplo de 9
Divisibilidad por 10
Son divisibles por 10 todos los números terminados en cero.
Por ejemplo:
20, 30, 100, 1.300, son divisibles por 10 ya que terminan en cero.
Tabla de números primos menores de 300
2
|
3 |
5 |
7 |
11
|
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
97 |
101 |
103 |
107 |
109 |
113 |
127 |
131 |
137 |
139 |
149 |
151 |
157 |
163 |
167 |
181 |
191 |
193 |
197 |
199 |
211 |
223 |
227 |
229 |
233 |
239 |
241 |
251 |
257 |
263 |
269 |
271 |
277 |
281 |
283 |
293 |
Números compuestos
Es aquel que tiene más de dos factores. Por ejemplo, el 12 es compuesto, porque se puede descomponer
en más de dos factores.
12 = 1 • 12
12 = 4 • 3
12 = 6 • 2
Todo número compuesto se puede
expresar como el producto de números
primos:
21 = 7 • 3
En este caso el 7 y el 3 son factores primos.
Un número natural se ha factorizado en forma completa cuando está ex presado como producto de números primos.
- Forma abreviada para factorizar
Dividir el número por el menor
número primo por el cual sea divisible y
así sucesivamente cada cuociente se va dividiendo por un número
primo
hasta obtener cuociente 1.
Los factores son todos los números primos usados como divisores. 1
Ejemplos:
Factorizar 48:
48 : 2
24 : 2
12 : 2
6 : 2
3 : 3
1
Luego,48 = 2 • 2 • 2 • 2 • 3 = 24 •
3
Factorizar 136
136 : 2
68 : 2
34 : 2
17 : 17
1
Luego, 136 = 2 • 2 • 2 • 17 = 23 • 17